Evolution of Maps and Gridding Systems

The earliest maps were painted on cave walls with organic dyes in 16,500 BCE. As human civilization evolved, so did our maps. From clay tablets in ancient Babylonia around 600 BCE to Anaximander’s first paper map in Ancient Greece, mapping evolved significantly. The earliest instance of using latitude and longitude in maps can be found in Ptolemy’s ‘Geographia’ around 100 AD.  The ‘Age of Exploration’ that spanned from the 14th century to the 16th century saw Nicholas Germanus invent the Donis map projection with equidistant parallels and meridians that converged toward the poles. Dr. John Snow came up with the earliest version of a concept we now know as the Geographic Information System (GIS).  From the advent of aerial photography (from planes) in the 20th century to the invention of satellite and drone technology in the 21st century, mapping has come a long way. Just like mapping, the gridding systems have also metamorphosed with advancing times.

Let us first understand what gridding is.

What is a Grid?

The earth is divided into rectangular shapes of different sizes based on latitude and longitude.

The largest one is continental sizes with pression 1; approximately 32 grids of pression 1 cover the globe. These grids are again subdivided into grids of pression 2 and so on. There are 12 such pressions. Every grid has a unique geohash (a string representing the location). These hashes are stored in databases since databases can easily handle ‘strings’ instead of two ‘floating-point’ numbers(latitude, longitude). As the precision increases, so does the geohash length. 

 

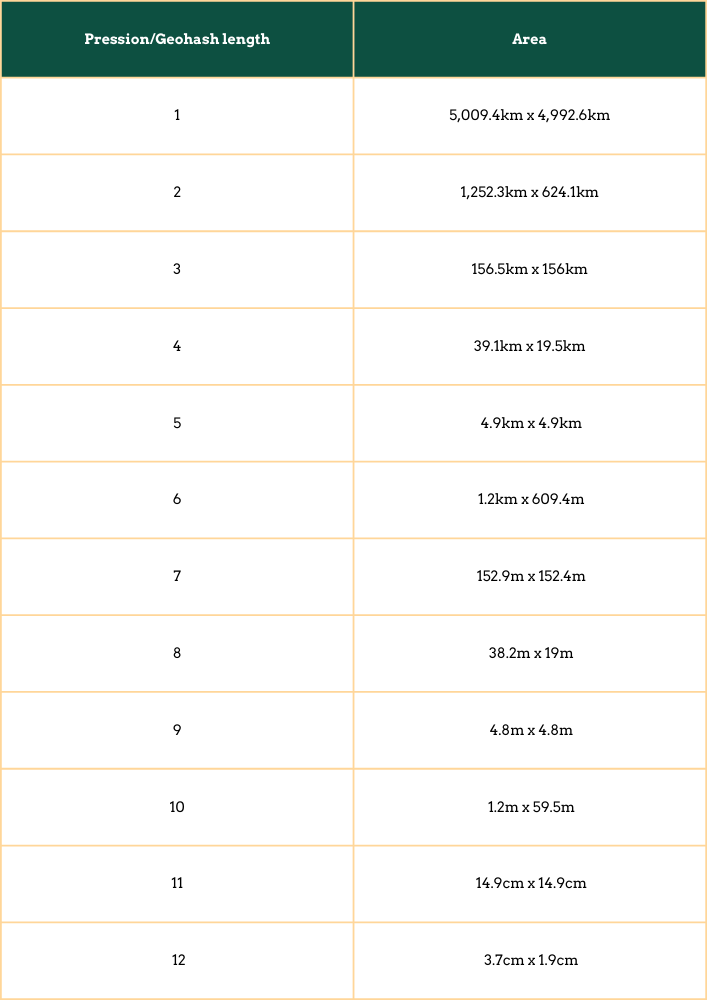
Pression vs. Area:

 

 

Execution of grids:
Many open-source packages support grid implementation for various programming languages. These packages provide functions to encode and decode latitude and longitude to hashes and vice versa. These grids are used for mapping POIs and other various indexes and can be used as required.

Drawbacks of Grids

• Edge Case Scenario: 

Geohashes can be used to find points in proximity to each other based on a common prefix. However, edge case locations close to each other but on opposite sides of the 180-degree meridian will result in Geohash codes with no common prefix (different longitudes for near physical locations). 

• Exception at poles:

Since the latitudes and longitudes converge at the poles, it is not easy to use the gridding system.
Points close to the North and South poles will have different geohashes (different longitudes for near physical locations).

• The Proximity Prefix Anomaly:

Two close locations on either side of the Equator (or Greenwich meridian) will not have an extended common prefix since they belong to different ‘halves’ of the world. Put simply, one location’s binary latitude (or longitude) will be 011111… and the other 100000…., so they will not have a common prefix, and most bits will be flipped.
This can also be seen as a consequence of relying on the Z-order curve (which could more appropriately be called an N-order visit in this case) for ordering the points, as two points close by might be visited at very different times. However, two points with an extended common prefix will be close to each other.

• The Z-order Curve problem:

To do a proximity search, one could compute the southwest corner (low geohash with low latitude and longitude) and northeast corner (high geohash with high latitude and longitude) of a bounding box and search for geohashes between those two. This search will retrieve all points in the z-order curve between the two corners, which can be far too many points. This method also breaks down at the 180 meridians and the poles. 

 

What is H3?

Imagine superimposing a bee-hive onto a world map to fragment the map into easy-to-understand cells. H3 allows us to do just that. 

H3 is a geospatial indexing system that partitions the world into hexagonal cells. H3 is open source under the Apache 2 licence developed by Uber to cater to its location data needs. The H3 Core Library implements the H3 grid system. It includes functions for converting from latitude and longitude coordinates to the containing H3 cell, finding the centre of H3 cells, finding the boundary geometry of H3 cells, finding neighbours of H3 cells, and more. Like grids, h3 cells are of the hierarchical order of resolution (0 to 15).

 

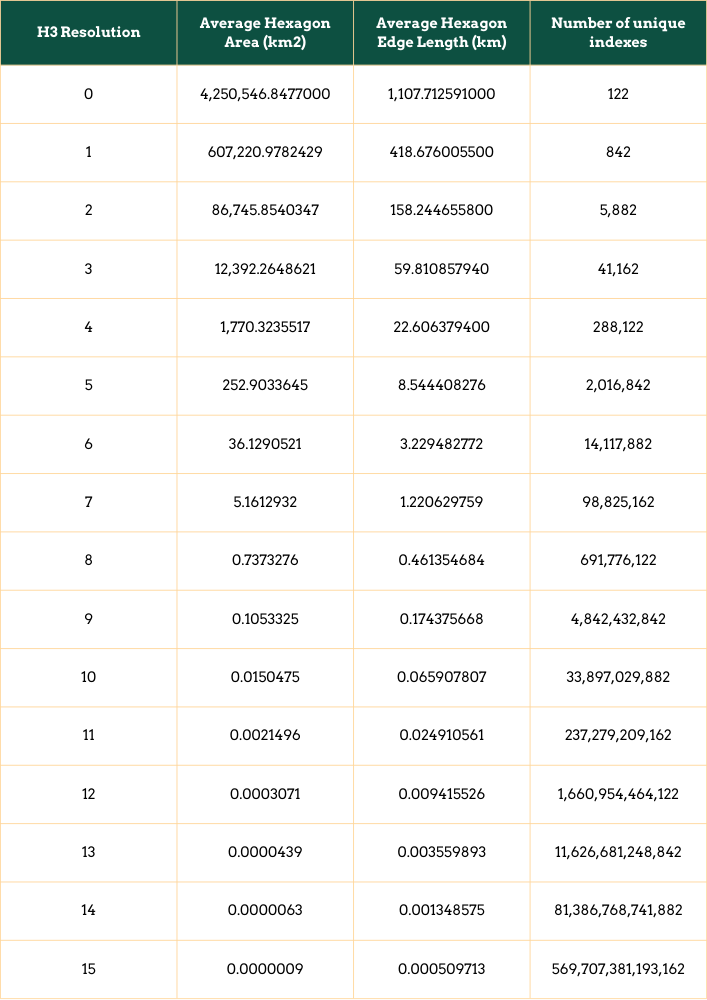
H3 Resolution and Coverage H3 Resolution:
As the resolution increases, the number of unique indices increases. At the macro level, 122 hexagons cover the surface of the Earth. As the granularity increases, the number of hexagons also increases.

 

 

Execution of H3:
h3-js is developed by Uber and provides all functionalities with Javascript support. H3 is used for decoding and encoding latitude and longitude to a 16-bit h3 hash and vice-versa. These h3 hashes are stored along with geo-boundary coordinates, which are used to plot on the map view. Then, these h3 are used for mapping POIs and various index values.

Head to Head: Grid vs. H3

Area distortion:​

Geohash encodes latitude and longitude pairs, and it is subject to significant differences in the area at different latitudes. A degree of longitude near a pole represents a significantly smaller distance than a degree of longitude near the Equator. In H3, on the other hand, we notice that there is negligible area distortion because it uses hexagons. H3 also uses 5 pentagons with 122 hexagons, but the pentagons are placed in unimportant places. It is located in the middle of the ocean; it does not hamper the analysis of essential areas.

 

Identifiers:​
Geohash uses strings for its cell indexes. Because they are strings, they can encode arbitrarily precise cells.

H3 cell indexes are designed to be 64-bit integers, which can be rendered and transmitted as strings if needed. The integer representation can be used when high performance is needed, as integer operations are usually more performant than string operations. Because indexes are fixed in size, H3 has a maximum resolution it can encode.

 

Better Visualisation and Spatial Analytics:
H3, a hexagonal & hierarchical system, allows better visualisation. In the unique use case of Uber Marketplace, it helped in demand sensing and driver & consumer analytics. Grids, on the contrary, do not provide us with similar benefits. Visualising and analysing grids can be somewhat of a tedious process.

 

Neighbourhood Search:
Since we use hexagons in H3, it is easier to search for the neighbours as a hexagon has precisely 6 neighbours. On the other hand, a triangle has 12, and a square has 8 neighbours. Thus, it is faster and has less time complexity, making it efficient.

Pinpoint Precision:
Suppose we require an exact containment, perhaps which has parcel data or political data where one cannot have an approximate containment. Still, if one needs to do this truncation, in that case, one might not want to use H3, or it might be highly complicated.H3 tries to be roughly equivalent, but innately it is not an equal area system. If a use case needs a pinpoint precision while performing a search, then H3 might not be the best fit. 

Thus, in the head to head of H3 and the traditional gridding system, H3 comes out as the go-to alternative for multiple reasons.